در علم اقتصاد «تئوری تولید» (Theory of Production) تلاش برای توضیح اصولی است که بر اساس آن یک شرکت تجاری تصمیم می‌گیرد چه مقدار از هر کالایی که می‌فروشد را تولید کند و برای تولید این کالا چه مقدار نیروی کار و سرمایه به کار ببرد. این نظریه شامل برخی از اساسی‌­ترین اصول علم اقتصاد است. این اصول شامل رابطه بین قیمت کالا و عوامل تولید مورد استفاده برای تولید کالا است. این اصول همچنین شامل روابط بین قیمت کالاها و عوامل تولید از یک طرف و مقادیر کالاها از سوی دیگر است. «تابع تولید» (Production Function) رابطه بین عوامل تولید (مانند نیروی کار و سرمایه) و خروجی را با فرض ثابت ماندن سطح تکنولوژی و استفاده از کارآمدترین روش تولید نشان می­‌دهد. در این نوشتار مفهوم تابع تولید  و انواع مختلف آن شرح داده خواهد شد.

تابع تولید چیست ؟

«تابع تولید» (Production Function) تابعی است که ارتباط بین مقدار عوامل تولید (مانند نیروی کار و سرمایه) و مقدار محصول تولید شده را با فرض ثابت بودن سطح تکنولوژی و استفاده از کارآمدترین روش تولید نشان می­‌دهد. به طور کلی، یک تابعِ تولید بیان‌گر رفتار بین نهاده‌های تولید و خروجی، به زبان ریاضی است. این مفهوم را می‌توان در سطح شرکت به صورت منفرد، صنایع یا کل اقتصاد مورد بررسی قرار داد.

با در نظر گرفتن کیفیت محصول و قیمت عوامل تولید مورد استفاده، وظیفه بنگاه، تعیین ارزان‌­ترین ترکیب از عوامل تولید است که بتواند بازده موردنظر بنگاه را ایجاد کند. این وظیفه به بهترین شیوه توسط تابع تولید انجام می‌شود. به عبارتی دیگر ، تابع تولید در اقتصاد معادله‌ای است که رابطه بین مقدار عوامل تولید مورد استفاده (مانند کار و سرمایه) و میزان محصول به دست آمده را نشان می‌دهد.

بنابراین تابع تولید، مقدار محصولی که به‌ازای هر ترکیب از عوامل تولید می‌توان ایجاد کرد را نشان می‌دهد. فرض می‌­شود که عوامل تولید شامل نیروی کار (L) و سرمایه (K) هستند. بنابراین تابع تولید را به صورت زیر می­‌توان نشان داد:

ٰQ= F(L , K)

در این رابطه تعریف متغیرها به صورت زیر است.

• «Q»: مقدار تولید
• «L»: نیروی کار
• «K»: نیز سرمایه

تابعِ تولید کل اقتصاد را می‌توان به شکل زیر نشان داد.

Y = A.F(K , N)

در این رابطه:

• «Y»: تولید ناخالص داخلی
• «A»: شاخص بهره‌وری کلی در اقتصاد
• «K»: مقدار ورودی سرمایه (برحسب واحدهای فیزیکی یا به دلار) در اقتصاد
• «N»: تعداد کارگران شاغل در اقتصاد (به نفر)

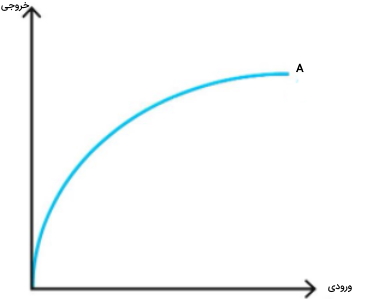
همچنین تابع تولید را می‌توان به صورتی گسترده‌تر به شکل زیر نشان داد.

$$Y= f(x_{1} +x_{2} + … x_{n}؛k_{1} +k_{2} + … k_{n})$$

در رابطه بالا Y، مقدار محصول (یا خروجی) را نشان می‌دهد. فرض بر این است که شرکت از n عامل متغیر تولید استفاده می‌کند. برای مثال عواملی مانند کارگران تولیدی که با دستمزد ساعتی کار می‌کنند یا مواد اولیه که مقدار آن‌ها قابل افزایش یا کاهش است. در فرمول بالا کمیت عامل متغیر اول با X1 تا Xn نشان داده شده است. همچنین فرض شده است که شرکت از m عامل ثابت یا عواملی مانند ماشین‌آلات ثابت، کارکنان حقوق‌بگیر و غیره استفاده می‌کند که مقادیر آن‌ها را نمی‌توان به آسانی یا به طور معمول تغییر داد.

فرمول بالا مقدار خروجی را به‌ازای مقادیر مشخصی از عوامل تولید نشان می‌دهد. به عنوان یک قاعده کلی، ترکیبات بسیاری از عوامل تولید وجود دارد که می‌توان از آن‌ها برای تولید همان مقدار خروجی استفاده کرد. به عبارتی برای تولید ۲ واحد از کالای فرضی X، می‌توان ۲ واحد نیروی کار و یک واحد سرمایه یا ۲ واحد سرمایه و یک واحد نیروی کار مورد استفاده قرار داد.

مساله کلیدی در توابع تولید، به حداقل رساندن هزینه تولید و یافتن ارزان‌ترین ترکیب از عوامل تولید است. بنابراین توابع تولید می‌توانند به سوالات مختلفی پاسخ دهند. برای مثال، این توابع می‌توانند بهره‌وری نهایی یک عامل تولید خاص را اندازه‌گیری کند. همچنین از تابع تولید می‌توان برای تعیین ارزان‌ترین ترکیب عوامل تولید که می‌توان برای تولید یک محصول به کار برد استفاده کرد. هزینه تولید شامل مجموع هزینه‌های کلیه عوامل تولید مختلف است. تابع هزینه را به صورت زیر می‌توان نوشت.

$$C= p_{1}x_{1} + …p_{n}x_{n} +r_{1}k_{1}+ …r_{n}k_{n}$$

در این رابطه تعریف متغیرها به صورت زیر است.

• «p1»: نشان‌دهنده قیمت یک واحد از اولین عامل متغیر
• «r1»: نشان‌دهنده هزینه سالانه نگهداری و مالکیت اولین عامل ثابت

به عبارتی هزینه تولید شامل دو بخش ثابت و متغیر است. بخش ثابت ارتباطی با تولید ندارد و مقداری ثابت است. بخش متغیر نیز با تغییر مقدار محصول، افزایش یا کاهش می‌یابد. براساس قانون بازدهی نزولی، افزایش پی در پی یک واحد از نهاده متغیر، مقدار تولید را در مرحله اول به مقدار زیادی افزایش می‌دهد و در مراحل بعدی به مقدار کم‌تری افزایش می‌یابد. با افزایش استفاده از نهاده، مقدار تولید کم‌تر و کم‌تر افزایش می‌یابد. به بیانی دیگر تولید با نرخی کاهنده افزایش می‌یابد. قانون بازدهی نزولی تنها در کوتاه‌مدت موضوعیت دارد و در بلند‌مدت مصداق ندارد.

 تابع تولید و مفهوم رشد

توابع تولید یک ابزار ادراکی هستند. این توابع یک عبارت مختصر ریاضی برای یک فرآیند ورودی-خروجی را به تصویر می‌کشند. استفاده از این توابع تا حد زیادی، برای توضیح رشد اقتصادی کشورها بوده است و به عنوان یک ابزار کلیدی، تئوری و حسابداری رشد را تشکیل داده است. توابع تولید به صورت کلی تلاشی برای توضیح عوامل موثر بر رشد اقتصادی در کشورهای مختلف هستند. این توابع همچنین نشان می‌دهند که چه چیزی نهاده‌های ورودی و خروجی را تنظیم می‌کند.

تصمیمات مختلفی که یک شرکت تجاری در مورد فعالیت‌های تولیدی خود اتخاذ می‌­کند در سه لایه پیچیده قابل طبقه‌بندی است.

1.  لایه اول: لایه اول شامل تصمیم‌­گیری در مورد روش‌های تولید مقدار معینی از محصول یک کارخانه با اندازه و تجهیزات معین است. این مساله را حداقل‌سازی «هزینه کوتاه‌مدت» (Short-Run Cost) می‌نامند.
2.  لایه دوم: این لایه شامل تعیین سودآورترین مقادیر محصولات برای تولید در هر کارخانه معین است که با حداکثرسازی سود در کوتاه‌مدت سروکار دارد.
3. لایه سوم: این لایه در مورد تعیین سودآورترین اندازه و تجهیزات کارخانه است که حداکثر کردن سود در بلندمدت نیز نامیده می­‌شود.

عوامل تولید چیست ؟

در اقتصاد کلان عوامل تولید به صورت زیر هستند.

• سرمایه فیزیکی (K): سرمایه فیزیکی یا دارایی‌های مشهودی که برای استفاده در فرآیند تولید ایجاد می‌شوند. این سرمایه‌ها شامل مواردی مانند ساختمان‌ها، ماشین‌ها، کامپیوترها و سایر تجهیزات هستند.
• نیروی کار (L): نیروی کار یا نهاده، فعالیت‌های ماهر و غیرماهر کارگران انسانی است.
• زمین (P): زمین که شامل منابع طبیعی، مواد خام و منابع انرژی مانند نفت، گاز و زغال سنگ است.
• کارآفرینی (H): کارآفرینی کیفیت هوش تجاری است که در عملکرد تولید اعمال می‌شود.

عوامل تولید در ساده‌ترین شکل، شامل زمین، نیروی کار و سرمایه هستند. زمین یک منبع طبیعی است که بنگاه اقتصادی برای تولید کالاها و خدمات جهت کسب سود استفاده می‌کند. زمین فقط به دارایی فیزیکی یا املاک محدود نمی‌شود. زمین شامل هرگونه منابع طبیعی مانند نفت خام، زغال‌سنگ، آب، طلا یا گاز طبیعی است. منابع نیز مواد طبیعی هستند که در تولید کالاها و خدمات استفاده می‌شوند.

نیروی کار نیز مقدار کاری است که کارگران انجام می‌دهند تا به فرآیند تولید کمک کنند. به‌عنوان مثال، اگر کارگری کار کند و تلاش او کالا یا خدمتی ایجاد کند، به منابع نیروی کار کمک کرده است. این تابع برای این که کاربرد عملی داشته باشد، باید دارای شکل و فرم مشخص باشد. یعنی باید قادر به توضیح فرآیند تبدیل ورودی‌ها به خروجی‌ها باشد. این تابع تلاش می‌کند حداکثر مقدار ستانده به‌ازای مقدار معینی نهاده ورودی را محاسبه کند.

سرمایه نیز هر ابزار، ساختمان یا ماشینی است که برای تولید کالا یا خدمات استفاده می‌شود. سرمایه در هر صنعتی متفاوت است. به عنوان مثال، یک برنامه‌نویس از کامپیوتر برای نوشتن برنامه استفاده می‌کند و سرمایه او کامپیوتری است که استفاده می‌کند. از طرف دیگر، یک آشپز از قابلمه و ماهی‌تابه برای آشپزی و ارائه کالا و خدمات استفاده می‌کند، بنابراین قابلمه و ماهی‌تابه، سرمایه آشپز محسوب می‌شوند.

در نهایت کارآفرین این عوامل تولید را برای کسب سود ترکیب می‌کند. به عنوان مثال، یک کارآفرین در زمینه جواهرات، نیروی کار و ماشین‌آلات را برای تولید جواهرات گرد هم می‌آورد و ریسک‌ها و مزایایی ناشی از تولید کالا را به عهده می‌گیرد. اکثر مکاتب اقتصادی انواع یکسانی از عوامل تولید، شامل زمین، نیروی کار، سرمایه و کارآفرینی (سرمایه‌فکری و ریسک‌پذیری) را شناسایی کرده‌اند.

مکاتب فکری پول‌گرایی، نئوکلاسیک و کینزی در مورد این که چه کسی باید مالک عوامل تولید و نقش آن‌ها در رشد اقتصادی باشد توافق دارند. مکاتب مارکسیستی و نئوسوسیالیستی استدلال می‌کنند که عوامل تولید باید ملی شوند و رشد در درجه اول، از سرمایه ناشی از کار حاصل می‌شود. مکتب اتریشی نیز بیان می‌کند که ساختار عوامل تولید، چرخه‌های تجاری را تعیین می‌کنند.

بحث اصلی بین سرمایه‌داری و سوسیالیسم در مورد مالکیت عوامل اولیه تولید است. نظام سرمایه‌داری بر این باور است که مالکیت خصوصی شرط لازم برای رقابت، نوآوری و رشد اقتصادی پایدار است. سوسیالیست‌ها استدلال می‌کنند که انباشت سرمایه خصوصی منجر به اختلاف ثروت کنترل نشده و تمرکز قدرت در دستان معدودی از افراد خواهد شد. مکتب اتریشی‌ استدلال می‌کنند که مدل‌های معمولی کینزی و نئوکلاسیک تا حد زیادی ناقص هستند و نمی‌توانند فرآیند مالکیت عوامل تولید و اهداف آن را به خوبی تبیین کنند.

مفهوم تابع تولید

تابعِ تولید روشی برای محاسبه ستانده تولید در مقایسه با ورودی آن است. شما نمی‌توانید از هیچ، چیزی بسازید. شما به لوازم، تجهیزات، منابع و مقداری دانش نیاز دارید. این که چقدر از این نهاده‌ها نیاز دارید می‌تواند بر تولید شما تأثیرگذار باشد. همان‌طور که اشاره شد در علم اقتصاد، تابعِ تولید راهی برای محاسبه ستانده نسبت به نهاده‌های ورودی است. در مجموع، تابعِ تولید فرآیند تبدیل فیزیکی ورودی‌ها به خروجی‌ها را به تصویر می‌کشد.

به‌عنوان مثال یک تابع فرضی تولید را می‌توان به صورت زیر نشان داد.

Q = f (K, L, P, H)

در این رابطه مقدار «تولید» (Q) تابعی از مقادیر ورودی ترکیب شده از هر عامل است. البته، همه مشاغل به عوامل تولید یا تعداد نهاده‌های یکسان نیاز ندارند. شکل دیگری از تابع تولید، نهاده‌ها را فقط به نیروی کار و سرمایه فیزیکی کاهش می‌دهد. فرمول این شکل از تابع تولید به‌صورت زیر است.

Q = f(L, K)

در رابطه بالا نیروی کار (L) و سرمایه (K) دو عامل تولید هستند که بیشترین تأثیر را بر مقدار تولید دارند.

تولید کل، تولید نهایی و تولید متوسط

در بحث تولید مفاهیمی مانند تولید کل، تولید متوسط و تولید نهایی وجود دارد که برای فهم بهتر تابع تولید و همچنین مراحل تولید در کلیه توابع تولید ضروری هستند. در ادامه این تعاریف به صورتی خلاصه مرور خواهند شد.

تولید کل چیست ؟

تولید کل (Total Production |TP) مقدار تولید به ازای هر سطح از عامل تولید است.

تولید متوسط چیست ؟

تولید متوسط (Average Production |AP)  هر عامل تولید عبارت است از تولید کل تقسیم بر آن عامل تولید. به عنوان مثال تولید متوسط نیروی کار به صورت زیر محاسبه می‌شود.

$$AP_{l}= frac{Q}{L}$$

در این رابطه Q تولید کل و L تعداد نیروی کار است.

تولید نهایی چیست ؟

تولید نهایی (Margianl Production | MP) مفهومی است که به صورتی گسترده با تولید کل و تابعِ تولید در ارتباط است. تولید نهایی هر عامل تولید، مشتق مرتبه اول تابع تولید نسبت به آن عامل تولید است. در تعریفی دیگر، تولید نهایی یک عامل تولید به آخرین واحد تولید شده توسط آن عامل تولید اشاره دارد. به بیانی دیگر تولید نهایی نسبت تغییر در تولید کل تقسیم بر تغییر در عامل تولید مورد نظر است.

$$MP{l}= frac{dQ}{dL}$$

در رابطه بالا dQ، تغییر در تولید کل و dL نیز تغییر در نیروی کار است که نشان‌دهنده مشتق جزئی Q نسبت به L است. به عنوان مثال، شرکتی به نام Z را در نظر بگیرید. وقتی کارخانه‌ای نیروی کار نداشته باشد، با وجود هر مقدار سرمایه فیزیکی، ستاده‌ای وجود نخواهد داشت. وقتی یک کارگر استخدام می‌شود، سه واحد در هر ساعت کار، تولید می‌شود. وقتی دو کارگر استخدام می‌شود، ستاده کل به پنج واحد در ساعت افزایش می‌یابد.

اضافه شدن کارگر دوم منجر به دو واحد بیشتر، در هر ساعت کار شده است. به بیانی دیگر تولید نهایی کارگر دوم برابر با ۲ واحد بوده است. از آن‌جا که تولید نهایی، رابطه مستقیمی با افزایش نیروی کار دارد، به آن تولید نهایی نیروی کار نیز گفته می‌شود. اگر افزایش تولید در نتیجه فناوری جدید یا سرمایه فیزیکی باشد، این تغییر در تولید را، تولید نهایی سرمایه می‌نامند. هنگامی که MP شروع به کاهش می‌کند، گفته می‌شود که قانون بازدهی نزولی شروع به عمل کرده است.

مراحل تولید

بر اساس منحنی‌های تولید کل (TP)، تولید متوسط (AP) و تولید نهایی (MP)، فرآیند تولید را به سه مرحله تقسیم می‌کنند. این مراحل در نمودار زیر نشان داده شده است.

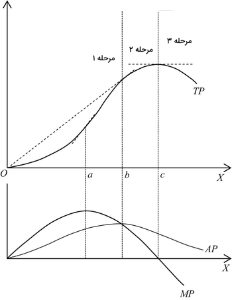
1. مرحله اول: از نهاده متغیر به حدی استفاده می‌شود که تولید متوسط در حال افزایش باشد. در این نقطه تولید نهایی بیشتر از تولید متوسط است.
2. مرحله دوم: از جایی شروع می‌شود که تولید نهایی برابر تولید متوسط است. در این نقطه تولید متوسط نیز حداکثر است. سپس تولید نهایی کوچکتر از تولید متوسط می‌شود و در نهایت در نقطه‌ایی که تولید نهایی برابر صفر می‌شود این مرحله به پایان میرسد.
3. مرحله سوم: در این مرحله، تولید نهایی منفی است. بنگاه هیچ‌گاه در مرحله سوم تولید نمی‌کند، زیرا تولید نهایی نیروی کار (MPL) منفی است. به عبارتی، حتی اگر نیروی کار رایگان باشد، بنگاه تا جایی نیروی کار استخدام می‌کند که MPL برابر با صفر شود یا تولید کل حداکثر گردد. اگر MPL منفی باشد، استخدام نیروی کار بیشتر، تولید کل را کاهش می‌دهد. بنابراین در این نقطه، حتی در صورت مجانی بودن نیروی کار، نباید نیروی کار جدید استخدام کرد.

با توجه به اهمیت موضوع تابع تولید و مفاهیم مرتبط با آن که نقش زیادی در فهم مسائل مربوط به اقتصاد صنعتی دارند، «سایت» اقدام به انتشار فیلم آموزش اقتصاد صنعتی کرده که لینک آن در ادامه آورده شده است.

بازده نسبت به مقیاس چیست ؟

در اقتصاد، «بازده نسبت به مقیاس» (Returns to Scale) نشان می‌دهد که با افزایش مقیاس تولید و نهاده‌های مربوط به عوامل تولید، چه اتفاقی برای ستاده یا تولید خواهد افتاد. مفهوم بازده نسبت به مقیاس در زمینه عملکرد تولیدی یک شرکت به وجود می‌آید. در بلندمدت، همه عوامل تولید متغیر هستند. این عوامل در پاسخ به افزایش معینی در مقیاس تولید، تغییر می‌کنند.

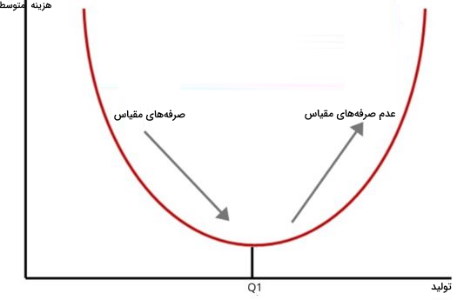
صرفه‌‌های نسبت به مقیاس اثر افزایش سطح تولید را بر هزینه‌های واحد تولیدی نشان می‌دهد اما بازده نسبت به مقیاس تنها بر رابطه بین مقادیر ورودی و خروجی متمرکز است. سه نوع بازده نسبت به مقیاس وجود دارد.

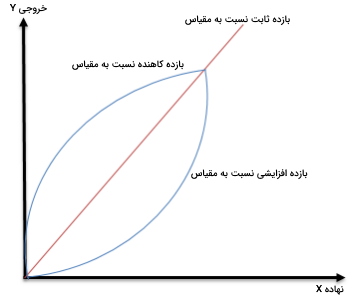
• بازده نسبت به مقیاس ثابت (Constant Returns to Scale): در صورتی که نهاده‌ها به نسبتی معین تغییر کنند و ستاده (خروجی) نیز با همان نسبت تغییر کند، بازده نسبت به مقیاس ثابت وجود دارد.
• بازده نسبت به مقیاس کاهشی (Decreasing Returns to Scale): در صورتی که نهاده‌ها به نسبتی معین تغییر کنند و ستاده (خروجی) با نسبتی کم‌تر تغییر کند، بازده نسبت به مقیاس کاهشی وجود دارد.
• بازده نسبت به مقیاس فزاینده (Increasing Returns to Scale): در صورتی که نهاده‌ها به نسبتی معین تغییر کنند و ستاده (خروجی) با نسبتی بزرگ‌تر تغییر کند، بازده نسبت به مقیاس افزایشی وجود دارد.

تابع تولید یک شرکت می‌تواند انواع مختلفی از صرفه‌های ناشی مقیاس را در محدوده‌های مختلف تولید نشان دهد. به بیانی دیگر، ممکن است در سطوح مختلف تولید، بازده نسبت به مقیاس، صعودی، نزولی و یا ثابت باشد. در اقتصاد خرد، بازده نسبت به مقیاس که یک شرکت با آن مواجه می‌شود، تا حد زیادی از نظر فن‌آوری تحمیل می‌شود و تحت تأثیر تصمیم‌های اقتصادی یا شرایط بازار قرار نمی‌گیرد. در ادامه یک مثال برای فهم بهتر انواع بازده مقیاس ارائه شده است. هنگامی که میزان استفاده از همه نهاده‌ها با ضریب 2 افزایش می‌یابد، مقادیر جدید ستاده به شکل زیر خواهد بود.

• ستاده دقیقاً با نسبت ضریب 2 افزایش پیدا کند: بازده نسبت به مقیاس ثابت
• ستاده با نسبتی بیشتر از ضریب 2 افزایش پیدا کند: بازده نسبت به مقیاس افزایشی
• ستاده با نسبتی کم‌تر از ضریب 2 افزایش پیدا کند: بازده نسبت به مقیاس ثابت

با فرض ثابت بودن هزینه‌های عوامل تولید و یکسان بودن تابعِ تولید، شرکتی که بازده ثابت نسبت به مقیاس را تجربه می‌کند، میانگین هزینه‌های بلندمدتِ ثابتی خواهد داشت. همچنین شرکتی که بازدهی نسبت به مقیاس کاهشی را تجربه می‌کند، میانگین هزینه‌های بلندمدت آن افزایشی خواهد بود و شرکتی که بازدهی نسبت به مقیاس فزاینده دارد، هزینه‌های متوسط بلندمدت را کاهش می‌دهد.

با این‌حال، اگر شرکت با بازار عوامل تولیدِ کاملاً رقابتی مواجه نشود، این رابطه از بین می‌رود. یعنی، قیمتی که شخص برای یک کالا می‌پردازد به مقدار خرید بستگی دارد. اگر شرکت بتواند برای خرید یک نهاده ورودی، تخفیف بزرگی دریافت کند، آن‌گاه می‌تواند در محدوده‌ای از سطح تولید که حتی بازده کاهشی وجود دارد، صرفه‌‌های مقیاس را  تجربه کند.

انواع توابع تولید

انواع مختلفی از توابع تولید وجود دارد. در این بخش مروری بر رایج‌ترین و پرکاربردترین توابع تولید در اقتصاد و ویژگی آن‌ها خواهد شد. مهم‌ترین توابع تولید به صورت زیر فهرست شده است.

• تابع تولید کاب-داگلاس
• تابع تولید کاب-داگلاس تعمیم‌یافته
• تابع تولید کشش جانشینی ثابت
• تابع تولید ترانسلوگ
• تابع تولید درجه دوم تعمیم یافته
• تابع تولید ترانسندنتال
• تابع تولید لئونتیف
• تابع تولید مرزی تصادفی
• تابع تولید همگن

در ادامه، این توابع و ویژگی‌های آن‌ها به صورت مختصر شرح داده خواهد شد.

تابع تولید کاب-داگلاس چیست ؟

«تابع تولیدِ کاب-داگلاس» (Cobb-Douglas Production Function) رابطه بین ستاده و نهاده‌های تولید را مدل‌سازی می‌کند. این تابع برای محاسبه نسبت ورودی‌ها به یکدیگر برای تولیدی کارآمد و تخمین تغییرات تکنولوژیکی در روش‌های تولید استفاده می‌شود. این تابع دو نهاده ورودی، نیروی کار و سرمایه برای تولید کل صنعت در نظر می‌گیرد. شکل کلی تابع تولید کاب-داگلاس به صورت زیر است.

$$Y=A L^{alpha}l^{beta}$$

در تابع تولید بالا تعریف متغیرها به صورت زیر است.

• «Y»: تولید کل
• «L»: نیروی کار
• «K»: سرمایه
• «A»: نیز تکنولوژٰی

همچنین $$alpha$$ و $$beta$$ نیز به ترتیب کشش نیروی کار و سرمایه هستند. این شکل از تابع تولید به افتخار ریاضی‌دان معروف «چارلز کاب» (Charles Cobb) و اقتصاددان نوبلیست «پل داگلاس» (Pole Douglas) به صورت «کاب-داگلاس» نام‌گذاری شده است.

تابع کاب-داگلاس نخستین بار برای در نظر گرفتن اهمیت نسبی دو نهاده نیروی کار و سرمایه در تابع تولید ایالات متحده، طی سال‌های 1899 تا 1924 استفاده شد. تابع کاب-داگلاس در مدل اصلی خود، پارامترهای کشش تولید α1 و α2 را به دامنه αi ∈ (0,1) محدود می‌کنند و مجموع کشش عوامل تولید را یک (1 = α1 + α2) در نظر می‌گیرد. این محدودیت که به معنای بازده ثابت به مقیاس در تابع کاب-داگلاس است. به عبارتی، مجموع کشش نیروی کار و سرمایه برابر با یک خواهد بود.

$$alpha + beta =1$$

در صورتی که از تابع بالا لگاریتم گرفته شود، شکل تابع به صورت زیر خواهد بود.

$$LnY = LnA + (alpha)LnL + (beta)Lnk$$

در صورت وجود داده‌های تولید، نیروی کار و سرمایه می‌توان پارامترهای A و $$alpha$$ و $$beta$$ را با استفاده از روش «حداقل مربعات معمولی» (Ordinary Least Squares | OLS) تخمین زد. در صورتی که بر اساس داده‌های واقعی، یک تابع کاب-داگلاس برآورد شود و برای $$alpha$$ مقدار 0/75 به دست بیاید، به این معنی است که نیروی کار ۷۵ درصد از ارزش تولید محصولات را در دوره مورد مطالعه به خود اختصاص داده است.

مقدار بودجه در دسترس و همچنین نسبت هزینه نهاده ورودی L به نهاده وردی K، ترکیب دقیق استفاده از نهاده‌های نیروی کار و سرمایه را برای تولید بهینه مشخص می‌کنند. شکل تابع تولیدِ کاب-داگلاس به صورت زیر است.

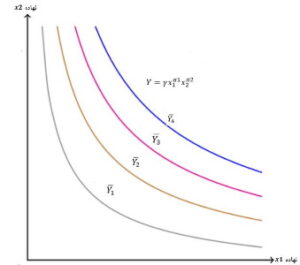
ویژگی های تابع تولید کاب-داگلاس

تابع کاب-داگلاس یکی از معروف‌ترین توابعی است که در بیان روابط ساختاری در تولید، از گذشته‌های دور مورد استفاده قرار گرفته است. این تابع بسیاری از خصوصیات تابع تولید نئوکلاسیک‌ها را در خود حفظ کرده است. پارامترهای تابع تولید کاب-داگلاس، کشش‌های تولید نهاده‌ها را به تصویر می‌کشد. محدودیت‌های ساختاری تابع کاب داگلاس، جذابیت آن را در مطالعات تجربی آکادمیک کاهش داده است.

از جمله محدودیت‌های این تابع می‌توان به ثابت بودن کشش‌های تولیدی نهاده‌ها در آن اشاره کرد. همچنین، تابع کاب-داگلاس فقط یک ناحیه تولید را برای هر نهاده نشان می‌دهد و نمی‌تواند سه ناحیه از تابع تولید را به تصویر بکشد. از سوی دیگر بازده نسبت به مقیاس در این تابع بدون توجه به سطح تولید تعیین می‌شود و کشش جانشینی آن نیز برابر عدد یک است. به عبارتی، تابع تولید کاب-داگلاس یک تابع تولید همگن از درجه یک است.

کاب و داگلاس بیان کردند که تابعِ تولید آن‌ها بر پایه‌های نظری محکمی استوار نیست و نباید آن را به عنوان قانون تولید درک کرد. این تابع فقط یک تقریب آماری از روابط مشاهده شده بین نهاده‌های تولید و ستاده را نشان می‌دهد. با این وجود، ویژگی‌های ریاضی ساده آن، برای اقتصاددانان جذاب است و منجر به تبدیل این تابع به یک مفهوم استاندارد در نظریه اقتصاد خرد در قرن اخیر شده است.

فرم تابع کاب-داگلاس نه تنها در نظریه تابع تولید استفاده می‌شود بلکه در نظریه رفتار مصرف‌کننده اقتصاد خرد نیز به صورتی گسترده به کار می‌رود. شکل‌های مختلفی از تابع تولید کاب-داگلاس وجود دارد. در ادامه برخی از مهم‌ترین شکل‌های تابع تولید کاب-داگلاس ارائه شده است.

تابع تولید کاب-داگلاس تعمیم یافته چیست ؟

تابع کاب-داگلاس با n نهاده ورودی را «تابع تولید کاب-داگلاس تعمیم‌یافته» (Generalized Cobb–Douglas Production Function) می‌نامند.  کاربردها و مزایای تابع کاب-داگلاس تعمیم‌یافته به دلیل امکان وارد کردن چندین نهاده ورودی به مدل، بسیار بیشتر از تابع کاب-داگلاس معمولی است. البته تابع کاب-داگلاس تعمیم‌یافته فقط یک مرحله از مراحل سه‌گانه تولید را نشان می‌دهد و از این نظر محددیت دارد.

تابع تولید کشش جانشینی ثابت چیست ؟

ٰتابع تولید «کشش جانشینی ثابت» ( Constant Elasticity of Substitution, not one | CES) یکی از فرم‌های مورد توجه در مطالعات تجربی است که بیشتر خصوصیات تابع تولید نئوکلاسیک را در خود حفظ کرده است. این تابع در مطالعات تجربی و آکادمیک به شکلی گسترده مورد استفاده قرار می‌گیرد. این تابع هر سه نوع بازدهی نسبت به مقیاس و با هر درجه‌ای از همگنی را نشان می‌دهد. از محدودیت‌های فرم تابع تولید کشش جانشینی ثابت می‌توان به ثابت بودن کشش جانشینی بین دو نهاده در آن اشاره کرد که به نسبت نهاده‌ها بستگی ندارد و هر عددی از صفر تا بی‌نهایت را می‌تواند داشته باشد. همچنین همانند تابع کاب-داگلاس، این تابع نیز تنها یک ناحیه از نواحی سه‌گانه تولید نئوکلاسیک‌ها را نشان می‌دهد.

تابع ترانسلوگ چیست ؟

تابع «ترانسلوگ» (Translog) تا حد زیادی بسیاری از ویژگی‌های تابع تولید نئوکلاسیک‌ها را تامین می‌کند. از مشخصات این تابع آن است که اجازه می‌دهد کشش‌های جانشینی و کشش‌های تولیدی، بسته به سطح مصرف نهاده‌ها، تغییر کنند. علاوه بر این، مشتق اول این تابع محدودیتی از نظر علامت ندارد. به عبارت دیگر، تابع ترانسلوگ هر سه ناحیه تولیدی را نشان می‌دهد و تولید نهایی در آن می‌تواند فزاینده، کاهنده و یا منفی باشد. در تابع ترانسلوگ علاوه بر پارامترهای متغیر‌های اصلی، ضرایب روابط متقابل متغیرها نیز قابل برآورد است.

تابع درجه دوم تعمیم یافته چیست ؟

«تابع درجه دوم تعمیم‌یافته» (Generalized Quasi-Function) بسیاری از ویژگی‌های تابع تولید نئوکلاسیک‌ها را تامین می‌کند. علاوه بر این، مانند تابع تولید ترانسلوگ، کشش‌های تولیدی در این تابع نیز بستگی به میزان مصرف نهاده‌ها دارد و مشتق اول آن محدودیتی از نظر علامت ندارد. این تابع می‌تواند نواحی سه‌گانه تولید را نشان دهد. در این تابع نیز پارامترهای روابط متقابل نهاده ها برآورد می‌شود و در نتیجه امکان ارزیابی همزمان اثر متقابل نهاده‌ها بر یکدیگر فراهم شده است.

تابع تولید لئونتیف چیست ؟

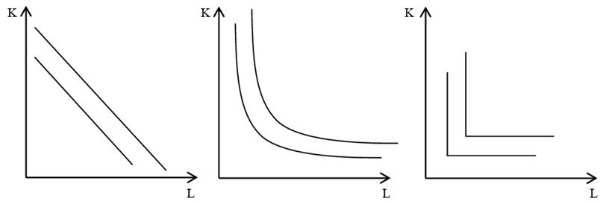
در علم اقتصاد، «تابع تولید لئونتیف» (Leontief Production Function) یا «تابع تولیدِ نسبت ثابت»، تابعی است که در آن عوامل تولید در نسبت‌های ثابت استفاده می‌شوند. در این تابع هیچ جایگزینی بین عوامل تولید وجود ندارد. نام این تابع از «واسیلی لئونتیف» (Wassily Leontief) گرفته شده و یک شکل محدود شده از تابع تولید کشش جانشینی ثابت است. شکل تابع تولید لئونتیف به صورت زیر است.

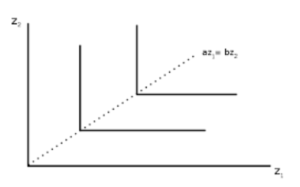
این تابع نیز به جز یک مورد، تمام خصوصیات تابع تولید نئوکلاسک‌ها را تامین می‌کند. سایر ویژگی‌های آن نیز مشابه تابع درجه دوم و ترانسلوگ است. مشتق اول تابع لئونتیف محدودیتی از نظر علامت ندارد و سه ناحیه تولید را نیز نشان می‌دهد.

تابع تولید ترانسندنتال چیست ؟

«تابع تولید ترانسندنتال» (Transcendental) شکل تغییر یافته‌ای از تابع تولید کاب-داگلاس است که کلیه ویژگی‌های تابع تولید نئوکلاسیک‌ها را تامین می‌کند. علاوه بر این، تابع کاب-‌داگلاس بخشی از تابع ترانسندنتال محسوب می‌شود که با وضع محدودیت‌هایی به دست آمده است. از همین‌رو امکان آزمون برتری یکتابع را بر تابع دیگر به راحتی فراهم می‌آورد. کشش‌های تولیدی نهاده‌ها در این فرم ثابت نیست ولی مقدار آن‌ها تنها به میزان مصرف همان نهاده بستگی دارد.

از خصوصیات مطلوب دیگر این تابع آن است که بازده نسبت به مقیاس در آن ثابت نیست و بستگی به مقدار مصرف نهاده دارد. به علاوه این فرم سه ناحیه تولیدی نئوکلاسیک‌ها را نشان می‌دهد. با توجه به این ویژگی‌ها، تابع ترانسندنتال را می‌توان یکی از فرم‌های مناسب برای بیان روابط تولیدی بر اساس نظریه تولید نئوکلاسیک‌ها دانست.

تابع تولید مرزی تصادفی چیست ؟

اهمیت «تابع تولیدِ مرزی تصادفی» (Random Frontier Production Functions) در پیش‌بینی کارایی فنی شرکت‌های منفرد در یک صنعت است. تابع مرزی، یک مرز را توصیف می‌کند که نشان‌دهنده حد خروجی قابل حصول از هر ترکیب ممکن از نهاده‌های ورودی است. به بیانی دیگر تابع تولید مرزی تصادفی، نشان‌دهنده مکان‌ هندسی بنگاه‌های کارا است که با استفاده از رویکردهای آماری برآورد می‌شوند. روش تحلیل مرزی تصادفی بیشتر برای تحلیل کارایی و رتبه‌بندی در شرکت‌های مختلف مانند بانک‌ها، موسسات مالی و دانشگاه‌ها استفاده می‌شود.

تابع تولید همگن چیست ؟

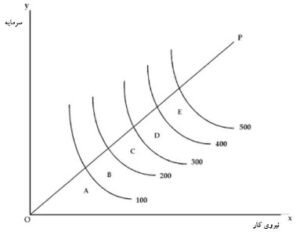
«تابع تولیدِ همگن خطی» (Linear Homogeneous Production Function) به این معنی است که با تغییر متناسب در همه عوامل تولید، خروجی نیز به همان نسبت افزایش یا کاهش می‌یابد. به عنوان مثال، اگر ضرایب نهاده‌های ورودی دو برابر شود، خروجی نیز دو برابر می‌شود. توابع تولید، زمانی همگن هستند که کشش جایگزینی آن‌ها برابر با یک باشد. تابع تولید همگن خطی را می‌توان در مطالعات تجربی مورد استفاده قرار داد زیرا می‌توان آن را به صورتی منطقی مدیریت کرد. به دلیل کاربردهای گسترده تابع تولید همگن، این تابع به طور گسترده در برنامه‌ریزی خطی و تحلیل ورودی-خروجی استفاده می‌شود. تابع تولید همگن خطی دارای بازدهی نسبت به مقیاس ثابت است. تابع تولید همگن را می‌توان به‌صورت زیر نشان داد.

nP=f(nK , nL)

در تابع بالا متغیرها به صورت زیر تعریف می‌شوند.

• «n»:  تعداد دفعات
• «nK»: تعداد دفعات افزایش عامل سرمایه
• «nL»: تعداد دفعات افزایش نیروی کار

تابع تولید همگن بدان معنا است که اگر همه عوامل تولید به شرط ثابت بودن قیمت به مقدار ثابتی افزایش یابند، تولید نیز به همان مقدار افزایش پیدا کند. تابع تولید همگن خطی را به شکل زیر می‌توان نشان داد. در تابع بالا نشان داده شده است که با تغییر نهادها با نسبت n، مقدار تولید نیز به همان اندازه تغییر کرده است.

معرفی فیلم آموزش اقتصاد صنعتی

در این نوشتار تلاش شد تا مروری بر مفهوم تابعِ تولید و همچنین ویژگی‌های خاص آن شود. همچنین انواع تابع تولید و خصوصیات آن نیز به جهت اهمیت آن مورد بحث و بررسی قرار گرفت. مبحث تابع تولید از مهم‌ترین و بنیادی‌ترین مباحث اقتصاد خرد است که به صورتی گسترده در سایر گرایش‌های اقتصاد نیز به‌کار می‌رود.

یکی از پرکاربردترین گرایش‌ها که تابع تولید به صورتی کاربردی و تجربی در آن مورد بحث و بررسی قرار می‌گیرد، اقتصاد صنعتی است. برای این منظور سایت اقدام به تهیه یک فیلم آموزشی ۶ ساعت و ۳۶ دقیقه‌ای در زمینه آموزش اقتصاد صنعتی کرده است.

این فیلم در ۹ درس ارائه شده است. در درس اول مفاهیم و تعاریف مرتبط با اقتصاد صنعتی مرور شده است. در درس دوم نیز مبحث بسیار مهم رقابت و انحصار در اقتصاد صنعتی بررسی می‌شود. درس‌های سوم تا پنجم نیز در زمینه ساختار بازار است که مواردی از جمله عرضه و تقاصا، صرفه‌های مقیاس، موانع ورود به بازار و همچنین تمرکز بازار را پوشش می‌دهد.

درس ششم مربوط به نظریه بازی‌ها و کاربردهای آن در بحث بازارها است. دروس هفتم و هشتم نیز کاربرد نظریه بازی در قیمت‌گذاری و عملکرد را مرور می‌کند. درس پایانی این فیلم آموزشی به بررسی دیدگاه اسلام در زمینه اقتصاد صنعتی و مباحث مربوط به رقابت و انحصار اختصاص پیدا کرده است. در تمامی فصل‌های مورد بررسی در این فیلم آموزشی نقش تابع تولید و مفاهیم مرتبط با آن از دیدگاه اقتصاد صنعتی بحث خواهد شد.

جمع‌بندی

در این نوشتار مفهوم تابعِ تولید و اجزای آن و همچنین دیدگاه‌های مختلف در زمینه آن مورد بحث و بررسی قرار گرفت. خلاصه نکات کلیدی و مفاهیم اصلی مربوط به آن رد ادامه فهرست شده است.

• تابعِ تولید: خروجی فیزیکی یک فرآیند تولید را به نهاده‌های فیزیکی یا عوامل تولید مرتبط می‌کند.
• هزینه نهایی: افزایش تولید همیشه با افزایش هزینه همراه است که می‌تواند با نرخی کاهنده یا افزاینده تغییر کند. هزینه نهایی، مشتق جزئی تابع هزینه نسبت به عامل موردنظر یا هزینه اضافی مربوط به تولید یک واحد خروجی بیشتر است.
• خروجی: خروجی اشاره به مقدار تولیدی دارد که ایجاد یا در حال تکمیل باشد.
• بازده مقیاس: بازده نسبت به مقیاس به سه دسته بازده ثابت، افزایشی و کاهشی طبقه‌بندی می‌شود.
• مراحل تولید: مراحل تولید براساس منحنی‌های تولید کل، تولید متوسط و تولید نهایی شامل سه مرحله اساسی است. بنگاه حتی در صورت رایگان بودن نیروی کار، در مرحله سوم تولید نمی‌کند.
• انواع توابع تولید: تابع تولید انواع بسیار مختلفی دارد اما پرکاربردترین توابع در اقتصاد شامل تابع تولید کاب-داگلاس، کشش جانشینی ثابت، لئونتیف، درجه دوم تعمیم‌یافته، ترانسلوگ و ترانسندنتال هستند.